| Chapitre 5. Oscillations mécaniques |
Oscillations mécaniques |
| OBJECTIFS | PRE-REQUIS | T D |
Oscillations libres
Oscillateur harmonique
Oscillateur amorti par forttement visqueux
Oscillations forcées
Caractéristique du
mouvement
Phénomène de résonance
Les mouvements oscillatoires sont fréquemment rencontrés dans la vie courante: tic-tac d'une montre, amortisseur de voiture, frémissement des feuilles au vent, etc. Il existe deux grandes catégories d'oscillations: libres ou forcées. Nous étudions dans une première partie les oscillations libres d'un système légèrement perturbé et qu'on laisse libre de retourner à sa position d'équilibre. En seconde partie, nous traitons les oscillations forcées qui font intervenir une source d'énergie extérieure et qui impose un mouvement oscillatoire au système étudié.
| Oscillations libres |
On entend par oscillations libres, le mouvement de systèmes oscillants qui après avoir subi une perturbation reviennent à leur position d'équilibre sans apport d'énergie extérieur. L'oscillateur fondamental est l'oscillateur harmonique.
| Oscillateur harmonique |
| Définition |
On appelle oscillateur harmonique tout système dont le paramètre ou degré de liberté x(t) qui caractérise son état au cours du temps s'écrit suivant la loi sinusoïdale :
|
|
Xm, w, j sont respectivement appelées amplitude, pulsation et phase à l'origine des temps. On a évidemment :
|
où T est la période, w la pulsation et n la fréquence.
L'oscillateur harmonique est un objet essentiel en physique car tout oscillateur quelconque peut être décomposé en oscillateurs harmoniques de différentes fréquences (ou pulsations).
| Equations différentielles caractéristiques |
L'application des lois de physiques (P.F.D., Théorème de l'énergie, du Moment cinétique, etc.) fournit généralement l'un des deux types d'équations différentielles suivantes :
|
|
On passe de la première à la seconde en multipliant par ![]() et en intégrant.
Réciproquement, on passe de la seconde à la première en dérivant et en simplifiant par
et en intégrant.
Réciproquement, on passe de la seconde à la première en dérivant et en simplifiant par
![]() .
.
| BIlan énergétique d'un oscillateur harmonique |
Considérons un oscillateur harmonique défini par un point
matériel M affecté d'une masse m, possédant un degré de liberté x,
soumis à une force conservative. L'énergie mécanique totale ![]() est constante et vaut :
est constante et vaut :
![]()
L'énergie potentielle est une fonction quadratique du degré de liberté et s'écrit :
|
|
L'énergie mécanique s'écrit :
![]()
comme ![]() , on obtient :
, on obtient :
![]() et
et ![]()
soit
|
|
L'énergie mécanique d'un oscillateur est une
constante proportionnelle au carré de la pulsation ![]() et au carré de l'amplitude
et au carré de l'amplitude ![]() .
.
| Oscillateur amorti par frottement visqueux |
| Bilan des forces appliquées au système |
Au cours du mouvement de l'oscillateur, on observe généralement que l'amplitude des oscillations n'est pas constante, mais décroît constamment. Cette décroissance de l'amplitude, ou perte d'énergie s'explique par l'action d'une force dont le travail est résistif et qui peut se mettre sous la forme :
![]()
proportionnelle à la vitesse et appelée force de frottement visqueux. Elle rend simplement compte des échanges d'énergie avec l'extérieur (frottement sur le sol rugueux, frottement de l'axe du pendule mécanique, frottement de l'air, etc.) et traduit le fait que plus le point se déplace rapidement, plus la force de frottement est importante et s'oppose au mouvement. Sans restreinte la généralité du problème, nous étudierons le problème des oscillations harmoniques par le cas particulier du ressort élastique.
| Equation différentielle du mouvement |
On considère une masselotte M de masse m accrochée à un ressort de raideur K. Les forces T de rappel et F de frottement appliquées en M sont portées par l'axe Ox de vecteur unitaire ex :

Compte tenu que le poids P et la réaction R du sol s'annulent réciproquement, le principe fondamental de la dynamique projetée sur l'axe Ox conduit à l'équation différentielle à laquelle satisfait la valeur X de l'élongation du ressort.
|
avec ![]() et
et ![]()
| Nature du mouvement |
On cherche les solutions de l'équation en ![]() . En remplaçant dans
l'équation canonique, on obtient l'équation caractéristique du second degré :
. En remplaçant dans
l'équation canonique, on obtient l'équation caractéristique du second degré :
![]()
qui admet comme solution la combinaison linéaire suivante :
|
|
r1 et r2 étant les solutions de l'équation du second degré :
 et
et
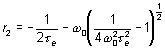
Suivant les valeurs sans dimension du
produit ![]() , on
distingue trois mouvements.
, on
distingue trois mouvements.
| Oscillateur faiblement amorti |
Cela correspond à ![]() ou
encore
ou
encore ![]() . On obtient
. On obtient
|
|
où w0, appelée pseudo-pulsation du mouvement est définie par :
![]()
Les quantités C et j sont déterminées à
partir des conditions initiales. Au bout d'un temps te l'amplitude est divisée par ![]() . La quantité te est
caractéristique de la durée de vie de ces oscillations amorties et on l'appelle durée
de relaxation en énergie. La courbe suivante représente les variations de x(t)
en fonction du temps. L'enveloppe décroît exponentiellement.
. La quantité te est
caractéristique de la durée de vie de ces oscillations amorties et on l'appelle durée
de relaxation en énergie. La courbe suivante représente les variations de x(t)
en fonction du temps. L'enveloppe décroît exponentiellement.
| Oscillateur très amorti |
Nous avons alors ![]() soit
soit ![]() . D'où :
. D'où :
|
|
Les constantes C1 et C2 sont également déterminées par les conditions initiales et mènent généralement vers des combinaisons de cosinus et sinus hyperboliques.
| Amortissement critique |
Nous avons ![]() . On obtient alors :
. On obtient alors :
|
Ce cas est qualifié de critique. C'est la position de réglage dans la pratique. On évite ainsi une trop longue attente de la position d'équilibre (amortisseur de voiture par exemple).
| Analogie mécanique |
En comparant les équations établies en Electricité et en Mécanique , on remarque l'analogie entre les différentes quantités physiques. Le tableau suivant résume les comparaisons.
Mécanique | x | v | a | m | K |
Electricité | q | i | R | L | 1/C |
| Oscillations forcées d'un pendule élastique |
Un oscillateur excité, soit par un déplacement de sa position d'équilibre soit d'une vitesse initiale non nulle, oscille et s'amortit du fait de la présence des forces de frottement qui dissipent l'énergie. Si maintenant, la force appliquée à l'oscillateur est elle-même oscillatoire, elle apporte périodiquement de l'énergie à l'oscillateur pour perpétuer le mouvement. L'étude suivante montre le comportement d'un oscillateur que l'on force à osciller sous l'action d'un excitateur.
| Caractéristique du mouvement |
| Equation différentielle du mouvement |
On considère un pendule élastique (m,
K) caractérisé par sa pulsation propre ![]() par sa durée de relaxation en énergie
par sa durée de relaxation en énergie ![]() , a étant le coefficient
de frottement visqueux. Supposons-le en outre soumis à une force excitatrice sinusoïdale
, a étant le coefficient
de frottement visqueux. Supposons-le en outre soumis à une force excitatrice sinusoïdale
![]() , de pulsation
, de pulsation ![]() et de phase à
l'origine
et de phase à
l'origine ![]() ,
, ![]() étant le vecteur
unitaire de l'axe Ox vertical descendant du référentiel terrestre R supposé
galiléen. La Loi fondamentale de la dynamique donne :
étant le vecteur
unitaire de l'axe Ox vertical descendant du référentiel terrestre R supposé
galiléen. La Loi fondamentale de la dynamique donne :
![]()
l0
est la longueur à vide du ressort. En posant ![]() et
et ![]() , l'équation prend la forme suivante :
, l'équation prend la forme suivante :
![]()
L'introduction des variables ![]() et
et ![]() prend en
compte le déplacement de l'origine vers le nouvel équilibre dû au poids et
l'élongation autour de la nouvelle position d'équilibre. L'équation précédente a donc
pour solution la position X(t) de M par rapport à cette
nouvelle origine.
prend en
compte le déplacement de l'origine vers le nouvel équilibre dû au poids et
l'élongation autour de la nouvelle position d'équilibre. L'équation précédente a donc
pour solution la position X(t) de M par rapport à cette
nouvelle origine.
| Position du point M |
Au bout d'un certain temps, le régime permanent s'installe. Seule la solution particulière subsiste. on aura alors X(t) de la forme :
![]()
Pour résoudre une telle équation on utilise la méthode complexe. On trouve alors :
et |
| Expression de la vitesse du point M |
Comme on a ![]() , on fait correspondre à la vitesse v(t)
une quantité complexe
, on fait correspondre à la vitesse v(t)
une quantité complexe ![]() tel que :
tel que :
![]()
![]() est l'amplitude complexe de la vitesse,
est l'amplitude complexe de la vitesse, ![]() l'amplitude et
l'amplitude et ![]() la phase à l'origine.
la phase à l'origine.
On obtient :
|
La vitesse est en avance de phase de ![]() par rapport à
l'élongation X.
par rapport à
l'élongation X.
| Impédance mécanique |
On appelle impédance mécanique ![]() le rapport de
l'amplitude complexe de la force excitatrice sur l'amplitude complexe de la vitesse :
le rapport de
l'amplitude complexe de la force excitatrice sur l'amplitude complexe de la vitesse :
|
|
D'après ce qui précède :
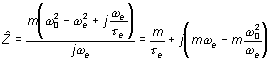
Si
![]() ,
,
on identifie :
|
|
| Puissance fournie par l'excitateur à l'oscillateur |
La puissance fournie par l'excitateur à
l'oscillateur, par l'intermédiaire de la force ![]() a pour expression :
a pour expression :
![]()
qui s'exprime à partir des quantités réelles. D'où :
![]()
en considérant la moyenne :
|
| Phénomène de résonance |
| Résonance en vitesse |
On appelle résonance en vitesse ou en puissance le transfert maximal de la puissance moyenne que fournit l'excitateur à l'oscillateur. Elle survient pour l'égalité :
![]()
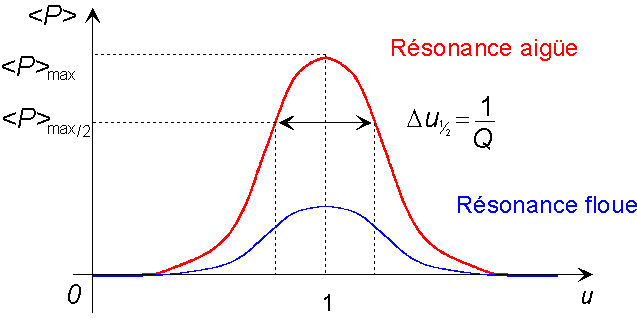
On évalue la finesse du pic de puissance en cherchant sa largeur totale à mi-hauteur. Les valeurs u pour lesquelles
![]()
sont telles que
![]() ou
encore
ou
encore ![]()
avec ![]() . A chaque valeur e correspond une racine positive et une négative. En ne conservant
que celles positives, on obtient :
. A chaque valeur e correspond une racine positive et une négative. En ne conservant
que celles positives, on obtient :
|
|
Remarquons que :
![]()
Comme ![]() , le facteur de qualité
s'écrit :
, le facteur de qualité
s'écrit :
|
|
C'est le rapport de la pulsation propre par
la largeur totale à mi-hauteur ![]() du pic de résonance. Un facteur qualité Q important
correspond à un pic étroit ou encore à une résonance aiguë, c'est-à-dire à un
oscillateur faiblement amorti(sismographe
du pic de résonance. Un facteur qualité Q important
correspond à un pic étroit ou encore à une résonance aiguë, c'est-à-dire à un
oscillateur faiblement amorti(sismographe ![]() ,
quartz piézo-électrique
,
quartz piézo-électrique ![]() ). Dans le cas contraire, on dit que la résonance est floue et
l'oscillateur correspondant est très fortement amorti.
). Dans le cas contraire, on dit que la résonance est floue et
l'oscillateur correspondant est très fortement amorti.
| Résonance en amplitude |
L'amplitude complexe de l'amplitude d'oscillations est donnée par :
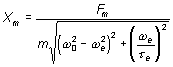
Lorsque la fréquence d'excitation ![]() est petite, proche de
0, l'amplitude de l'oscillateur
est petite, proche de
0, l'amplitude de l'oscillateur ![]() est quasi-constante et non nulle. Au contriare lorsque
est quasi-constante et non nulle. Au contriare lorsque ![]() est grande,
l'oscilateur n'a pas le temps de réagir à la sollicitation, donc
est grande,
l'oscilateur n'a pas le temps de réagir à la sollicitation, donc ![]() tend vers 0.
L'amplitude présente un maximum si le dénominateur possède un minimum. En dérivant le
dénominateur, on trouve :
tend vers 0.
L'amplitude présente un maximum si le dénominateur possède un minimum. En dérivant le
dénominateur, on trouve :
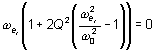
La première racine est
|
|
La deuxième n'existe que si ![]() , et vaut alors :
, et vaut alors :
|
|
Elle est d'autant plus proche de ![]() que Q est
grand, c'est-à-dire que le terme de frottement est faible.
que Q est
grand, c'est-à-dire que le terme de frottement est faible.
La figure suivante représente les différents cas possible en fonction de Q.

C.Péré. Esiea-ouest
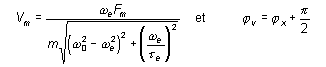
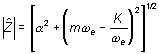 et
et