Chapitre 4. Forces centrales. Problème de Kepler |
Forces centrales. Problème de Kepler |
Rappels de mécanique classique
Force centrale
Repère barycentrique
Propriétés des
mouvements à force centrale
Conservation du moment
cintétique
Conservation de l'énergie
Problème de Kepler
Expression de
l'énergie potentielle newtonienne
Equation de la
trajectoire
Etude particulère de
l'état lié
Application
des lois de Kepler au système solaire et aux satellites artificiels
| Rappels de mécanique classique |
| Force centrale |
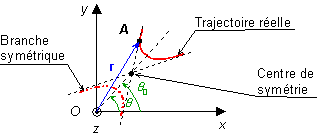
Le mouvement d'un point matériel A soumis à une force centrale est celui pour lequel la force passe par un centre O. Lorsque cette force dérive d'un potentiel (ou d'une énergie potentielle Ep), un tel mouvement est caractérisé par une énergie potentielle qui ne dépend que de la norme r du vecteur position r, soit :
|
L'importance de ces forces est considérable car leur étude concerne à
la fois les interactions gravitationnelles, électromagnétiques et fortes. Nous étudions
plus en détail le cas ![]()
| Repère barycentrique |
L'intérêt d’un tel repère repose sur
la réduction du problème à deux corps A1 et A2
de masse m1 et m2, à un problème à un corps A
de masse m, soumis de la part du centre de
masse C de ces deux points à la force d'interaction de ces deux points,
portée par le vecteur ![]() qui les relient.
qui les relient.
| Quantité de mouvement d'un système. Centre de masse |
La quantité totale du système ![]() dans un référentiel R, supposé galiléen, d'origine O,
est définie par :
dans un référentiel R, supposé galiléen, d'origine O,
est définie par :
![]()
Elle est égale à celle du centre de masse C affecté de la masse totale M. |
| Définition du référentiel barycentrique |
On appelle référentiel barycentrique
ou référentiel du centre de masse, le référentiel RG en translation par
rapport à R et tel que la quantité de
mouvement du système soit nulle, ![]() . Comme
. Comme ![]() , on
en déduit que
, on
en déduit que ![]() et que par conséquent,
le centre de masse est immobile dans RG.
et que par conséquent,
le centre de masse est immobile dans RG.
Le référentiel barycentrique RG est un référentiel galiléen. |
| Eléments cinétiques du système à deux corps |
Soit deux points A1 et A2 affectés respectivement des masses m1 et m2.
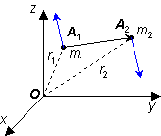
soit
![]()
![]() et
et![]()
Dans RG, la norme de la quantité de mouvement de chacune des particules est égale à celle d'une particule fictive A de masse m et de vitesse v.
L'énergie cinétique du système est la somme des énergies cinétiques des deux particules dans le R.B :
![]()
qui correspond à l'énergie cinétique d'une particule A de masse réduite m et de vitesse réduite v.
L'énergie potentielle du système est la somme des énergies potentielles des deux particules dans le R.B. En supposant des forces conservatives et un potentiel radial, l'énergie mécanique totale Em s'écrit :
![]()
C'est l'énergie mécanique d'une particule de masse m animée d'une vitesse v.
Intéressons-nous ensuite aux équations du
mouvement dans le référentiel RG, en supposant qu’il existe une force
d’interaction entre A1 et A2.
Soit la force ![]() appliquée par le point A2 sur le point
A1. On a, d’après le principe fondamental de la dynamique :
appliquée par le point A2 sur le point
A1. On a, d’après le principe fondamental de la dynamique :
![]()
Tout se passe comme si la particule de masse m
était soumise à la force centrale ![]() puisque portée par r. La particule A
est généralement différente des particules A1 et A2.
puisque portée par r. La particule A
est généralement différente des particules A1 et A2.
Il suffit alors de déterminer le mouvement de A par rapport à C dans le référentiel RG puis d’en déduire celui de A1 et de A2 également dans RG. Cela fait, par simple composition des mouvements , on repasse dans R puisque RG se déplace à vitesse constante dans R.
L’essentiel des problèmes que nous
aborderons concernent des masses telles que ![]() de sorte que
de sorte que ![]() . Dans ce cas,
. Dans ce cas,
![]()
soit
![]() et
et
![]()
La particule fictive A est confondue avec A2 et A1 coïncide pratiquement avec le centre de masse C du système. Cela veut également dire que RG et R sont confondus.
Pour la suite du cours, on déterminera
simplement le mouvement dans le référentiel barycentrique de centre O (![]() ) des deux points A1
et A2, c'est-à-dire la trajectoire de la
particule fictive A de masse réduite m.
) des deux points A1
et A2, c'est-à-dire la trajectoire de la
particule fictive A de masse réduite m.
| Propriétés des mouvements à force centrale conservative |
| Conservation du moment cinétique |
La force étant centrale, son moment au centre O est nul. Donc, le moment cinétique en O de la particule A, de masse m, dans le référentiel galiléen R, est constant, soit :
![]()
ou encore
![]()
d'où
![]()
Ce qui implique que le plan normal à L0 qui contient OA et vA est constant. La trajectoire est donc plane. Retenons donc que le mouvement d'un point matériel soumis à une force centrale est plan.
Dans la suite, par souci de simplification, on choisit l'axe Oz du référentiel R suivant L0 et on notera Oxy le plan dans lequel s'effectue le mouvement. En coordonnées polaires,
![]()
D'où :
![]() avec
avec ![]()
Pour des raisons historiques, on exprime parfois la conservation du moment cinétique à l'aide de la constante des aires
|
|
qui n'est autre que le moment cinétique par unité de masse, ou à l'aide de la vitesse aréolaire va
Cette relation représente l'intégrale première du mouvement.
| Conservation de l'énergie |
Exprimons, en coordonnées polaires, la conservation de l'énergie
mécanique de ce point matériel soumis à une force dérivant de l'énergie potentielle ![]() :
:
![]()
donne
|
|
qui est l'intégrale première de l'énergie.
En introduisant le carré de la norme du moment cinétique L2 et l'énergie potentielle effective :
![]()
avec ![]()
| Problème de Kepler |
On désigne par problème de Kepler le cas où l'interaction est newtonienne ou coulombienne.
de la forme ![]()
| Expression de l'énergie potentielle newtonienne |
Une interaction est newtonienne si la force F d'interaction
est en ![]() :
:
![]()
K étant positif ou négatif suivant que la force est répulsive ou négative. Rappelons que le travail élémentaire est :
![]()
soit
![]()
L'énergie potentielle est nulle à l'infini (hypothèse), ce qui entraîne une constante nulle. D'où :
|
|
L'énergie potentielle effective peut être positive ou négative :
![]()
selon que K est positif ou négatif. Cela correspond aux états libres ou liés de la particule soumis à ce potentiel.
| Equation de la trajectoire |
Pour déterminer la trajectoire, on doit utiliser la loi fondamentale de la dynamique ou ses conséquences. Utilisons par exemple les formules de binet ou la conservation de l'énergie mécanique (on rappelle que les forces mises en jeu sont conservatives et que l'on peut par conséquent utiliser cette propriété).
| Formules de Binet |
Les formules de Binet donnent les expressions de vA
et aA du point A en fonction des variables ![]() et q. En
coordonnées polaires, on a :
et q. En
coordonnées polaires, on a :
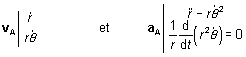
En exprimant ![]() en
cordonnées
en
cordonnées ![]() , on
obtient alors :
, on
obtient alors :
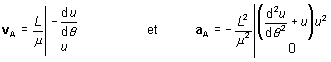
L'application du PFD donne alors l'équation différentielle à laquelle satisfait u.
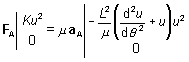
| Conservation de l'énergie mécanique |
On peut également trouver l'équation de la trajectoire à paritr de la conservation de l'énergie. On a:
![]()
Comme ![]() et compte tenu des résultats précédents. On obtient :
et compte tenu des résultats précédents. On obtient :
![]()
En dérivant par q, on obtient :
![]()
soit
|
|
en introduisant la quantité ![]() homogène à une longueur et
homogène à une longueur et ![]() (
(![]() ) selon que la force est répulsive ou attractive. L'équation
différentielle obtenue est du second ordre. La solution générale est la somme de la s.s.s.m
et d'une solution particulière :
) selon que la force est répulsive ou attractive. L'équation
différentielle obtenue est du second ordre. La solution générale est la somme de la s.s.s.m
et d'une solution particulière :
![]()
en posant ![]() , on obtient :
, on obtient :
|
|
Cette équation représente en coordonnées polaires une conique dont le centre O est l'un des foyers, p le paramètre de la conique et e l'excentricité.
Reprenons l'expression ![]() .
Avec celle de u ci-dessus, on obtient :
.
Avec celle de u ci-dessus, on obtient :
![]()
ou
|
|
| Discussion sur les valeurs de K |
Cas répulsif (K > 0)
Dans le cas ![]() , r
s'écrit :
, r
s'écrit :
![]()
Puisque ![]() , on a
, on a ![]() .
Le dénominateur peut donc s'annuler pour
.
Le dénominateur peut donc s'annuler pour ![]() et donner un rayon infini.
et donner un rayon infini.
La trajectoire est une hyperbole de foyer O |
|
Cas attractif (K < 0)
Dans le cas ![]() , r s'écrit :
, r s'écrit :
![]()
On distingue alors les états libres des états liés.
Les états libres sont tels que ![]() (
(![]() ).
).
La conique
est une hyperbole si |
|
Les états liés sont tels que ![]() ou
ou ![]()
La conique
correspondante est une ellipse si |
|
Les trois figures représentent les différents cas possibles.
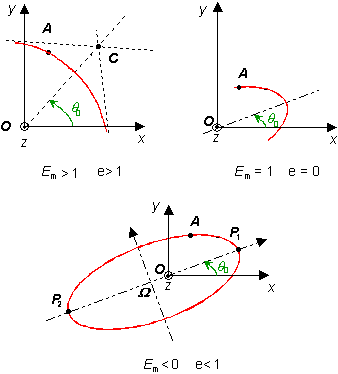
| Etude particulère de l'état lié |
Nous avons vu que les conditions d'un mouvement elliptique sont telles que
la force doit être attractive ![]() et l'énergie mécanique
et l'énergie mécanique ![]() négative mais supérieur à la valeur minimale E0
de l'énergie potentielle effective :
négative mais supérieur à la valeur minimale E0
de l'énergie potentielle effective :
![]()
![]()
v0 et r0 étant respectivement la vitesse et la position initiales.
| Caractéristiques de la trajectoire elliptique |
L'équation polaire de la trajectoire montre que sur l'ellipse de grand axe 2a :
![]() ,
,
![]() et
et ![]()
avec ![]() , soit :
, soit :
|
|
La distance ![]() du centre de l'ellipse W au centre de force O est
appelé distance focale et vaut :
du centre de l'ellipse W au centre de force O est
appelé distance focale et vaut :
![]()
soit
|
|
Enfin,
|
|
où b représente le demi-petit axe de l'ellipse.
| Equation cartésienne de la trajectoire |
Dans le système d'axes WXY, l'équation polaire s'exprime par ::
![]()
soit après transformations :
|
|
C'est l'équation d'un ellipse.
| Relation entre a et Em |
Comme ![]() , il vient :
, il vient :
|
|
L'énergie mécanique ne dépend que du grand axe de l'ellipse décrite.
| Période de révolution |
La vitesse aréolaire étant constante, la durée mise par un point A pour parcourir l'ellipse est une constante :
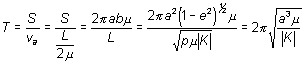
en remarquant que ![]() et
et ![]() .
.
On obtient ainsi :
|
|
Le carré de la période est proportionnel au cube du demi-grand axe de l'ellipse.
| Variation de la vitesse sur l'ellipse |
L'équation définissant l'énergie cinétique donne :
![]()
ou encore
|
|
Donc la vitesse est maximale au périgée (point le plus proche du centre O) et minimale à l'apogée (point le plus éloigné).
| Cas particulier où e est nulle |
Si ![]() , l'ellipse se réduit à un cercle de centre O
et de rayon r0 correspondant au minimum de l'énergie potentielle
effective :
, l'ellipse se réduit à un cercle de centre O
et de rayon r0 correspondant au minimum de l'énergie potentielle
effective :
![]() et
et ![]()
Comme
![]()
on a :
![]() soit
soit ![]()
D'où :
|
|
On retrouve ainsi une relation entre Ep, Ec et Em caractéristique du mouvement circulaire dans le problème de Kepler.
| Application des lois de Kepler au système solaire et aux satellites artificiels |
Ces lois sont au nombre de trois.
- 1ère loi : Les centres des planètes décrivent des ellipses dont le foyer est occupé par le soleil. - 2ème loi : Les rayons vecteurs balaient en des temps égaux des aires égales. - 3ème loi : Les rapports des carrés des périodes de révolution sur les cubes des demi grands axes sont indépendants de la planète. |
|
Le soleil est ainsi assimilé comme le centre attractif fixe O
dans le référentiel R. La masse de chaque planète est négligeable par rapport à celle
du Soleil ![]() . Ce qui
revient à considérer uniquement les interactions Soleil-Planètes . Le problème à N
planètes est réduit à N problèmes à deux corps, ce qui induit des trajectoires
elliptiques.
. Ce qui
revient à considérer uniquement les interactions Soleil-Planètes . Le problème à N
planètes est réduit à N problèmes à deux corps, ce qui induit des trajectoires
elliptiques.
Le moment cinétique étant constant au cours du temps, la vitesse aréolaire est constante, ce que traduit la deuxième loi.
Quant à la troisième, elle découle directement de l'expression de la période:
![]()
soit en négligeant la masse de la planète devant celle du soleil :
![]()
C.Péré. Esiea-ouest